[计算理论基础] 有穷自动机

确定性有穷自动机

定义2.1：确定性有穷自动机

$M=(Q,\Sigma, \delta, q_0, F)$

其中：

$Q$ ：有穷状态集
$\Sigma$ : 输入字母表
$\delta: Q \times \Sigma \to Q$ : 转移函数
扩展的转移函数： $\delta: Q \times \Sigma^* \to Q$
$q_0 \in Q$ : 初始状态
$F\subseteq Q$ : 接受状态
$L(M) = \{w\in \Sigma^*|\delta(q_0, w)\in F\}$ 为正则语言

正则运算

设 $A$ ， $B$ 为两个语言，正则运算为：

并 $A\cup B$
连接 $AB$
星号 $A^*$

定理：正则语言对正则运算封闭

定理：正则语言对补运算封闭
思路：证明补运算产生的语言和原来的语言互补
证明：设正则语言 $L=L(M)$ ,
$M=(Q,\Sigma, \delta, q_0, F)$ ，令 $F'=Q-F$ .
$M'=(Q,\Sigma, \delta, q_0, F')$ .
$\forall x, x\in L(M) \Leftrightarrow \delta(q_0,x)\in F \Leftrightarrow \delta(q_0,x)\notin F' \Leftrightarrow x \notin L(M')$ (证明互补)
所以 $L(M')=\Sigma^*-L(M) = L(M)^c$

定理2.12：正则语言对并运算封闭
思路：让两个自动机同时运行只要一个接受就接受
证明：设正则语言 $L_i=L(M_i)$ ,
$M=(Q_i,\Sigma_i, \delta_i, q_i, F_i), i=1,2$ .
$Q_3=Q_1\times Q_2; q_3=(q_1,q_2)$ ;
$\delta_3((r_1,r_2), a)=(\delta_1(r_1,a),\delta_2(r_2,a))$
$F_3=(F_1\times Q_2)\cup (Q_1\times F_2)$ .(F为接受状态，只要一个 $F_i$ 接受即可)
$M_3=(Q_3,\Sigma_3, \delta_3, q_3, F_3)$ .
$L_1\cup L_2=L(M_1)\cup L(M_2)=L(M_3)$

NFA证明：设 NFA $N_i=(Q_i,\Sigma, \delta_i, q_i, F_i)$ 识别 $A_i,i=1,2$ 构造 NFA N 识别 $A_1\cup A_2$
$Q=Q_1\cup Q_2 \cup \{q_0\}$
$F=F_1\cup F_2$
$\delta(q,a)=\left\{\begin{array}{ll} \delta_1(q,a) & q\in Q_1 \\ \delta_2(q,a) & q\in Q_2 \\ \{q_1,q_2\} & q=q_0\wedge a = \epsilon \\ \emptyset & q=q_0\wedge a \neq \epsilon \end{array}\right.$

定理：正则语言对交运算封闭
思路：1. 布尔运算(交并补)转为之前的问题。 2. 让两个自动机同时运行只要都接受就接受
证明：设正则语言 $L_i=L(M_i)$ ,
$M=(Q_i,\Sigma_i, \delta_i, q_i, F_i), i=1,2$ .
$Q_3=Q_1\times Q_2; q_3=(q_1,q_2)$ ;
$\delta_3((r_1,r_2), a)=(\delta_1(r_1,a),\delta_2(r_2,a))$
$F_3=F_1\times F_2$ .(F为接受状态，两个 $F_i$ 都接受)
$M_3=(Q_3,\Sigma_3, \delta_3, q_3, F_3)$ .
$L_1\cap L_2=L(M_1)\cap L(M_2)=L(M_3)$

推论：正则语言对布尔运算、差、对称差封闭

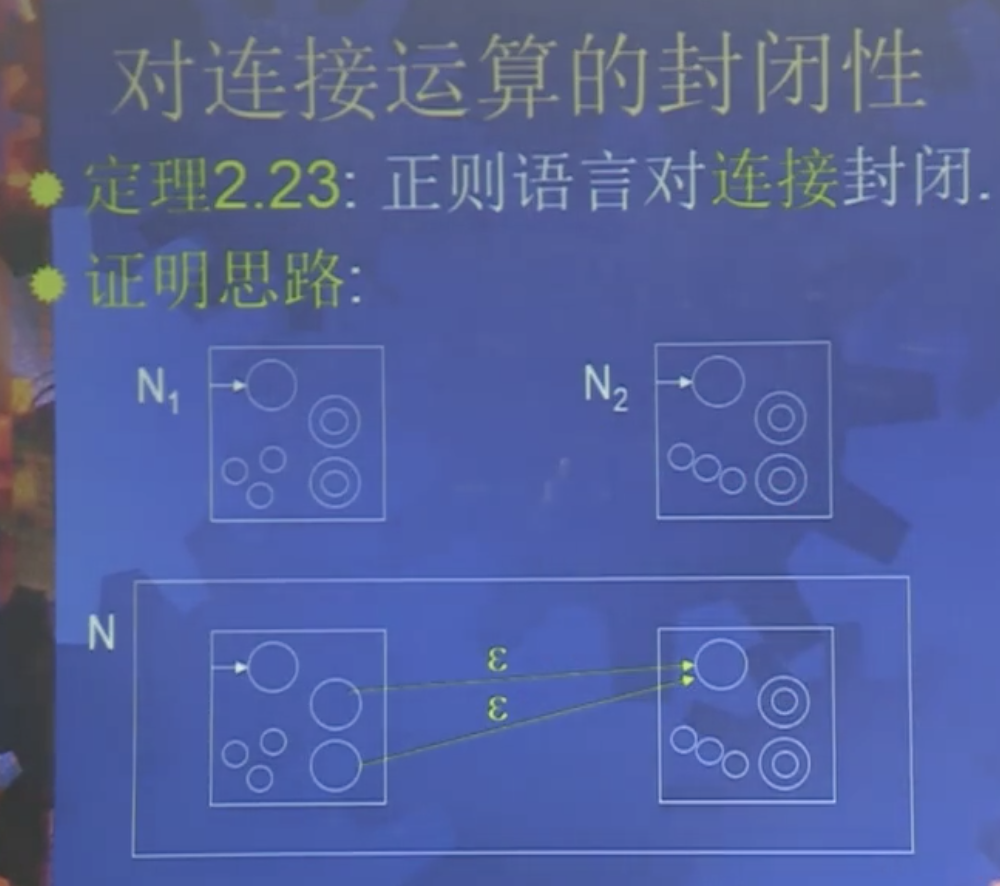
定理2.13：正则语言对连接运算封闭
思路：对于两个自动机 $A$ 和 $B$ ，一直运行 $A$ 直到所有串输入，过程中，当 $A$ 出现接受状态时，同步启动一个 $B$ 运行，最终根据是否有 $B$ 达到接受状态决定是否接受输入串。
证明：略。

NFA证明：
$Q=Q_1\cup Q_2$
$\delta(q,a)=\left\{\begin{array}{ll} \delta_1(q,a) & q\in Q_1,a\notin F_1 \\ \delta_1(q,a) & q\in F_1,a\neq \epsilon \\ \delta_1(q,a)\cup \{q_2\} & q\in F_1,a = \epsilon \\ \delta_2(q,a) & q\in Q_2 \end{array}\right.$

定理2.24：正则语言对星号运算封闭
思路：类似于定理2.13，初始状态集 $\{q_0\}$ ，当第一个自动机出现接受状态 $q_f$ 时，启动第二个自动机，并从当前输入开始运行所有自动机，状态集为 $\{q_f, q_0\}$ 当两个自动机中任一个出现接受状态则启动一个新的自动机，并从当前输入开始继续运行所有自动机 ( 例如， $\{q_x, q_f, q_0\}$ )，最终根据自动机状态集合中是否出现接受状态而接受。

NFA证明：
$Q=Q_1\cup \{q_0\}$
$F=F_1\cup \{q_0\}$
$\delta(q,a)=\left\{\begin{array}{ll} \delta_1(q,a) & q\in Q_1,a\notin F_1 \\ \delta_1(q,a) & q\in F_1,a \neq \epsilon \\ \delta_1(q,a)\cup \{q_1\} & q\in F_1,a = \epsilon \\ \{q_1\} & q=q_0,a=\epsilon \\ \emptyset & q=q_0,a\neq \epsilon \end{array}\right.$

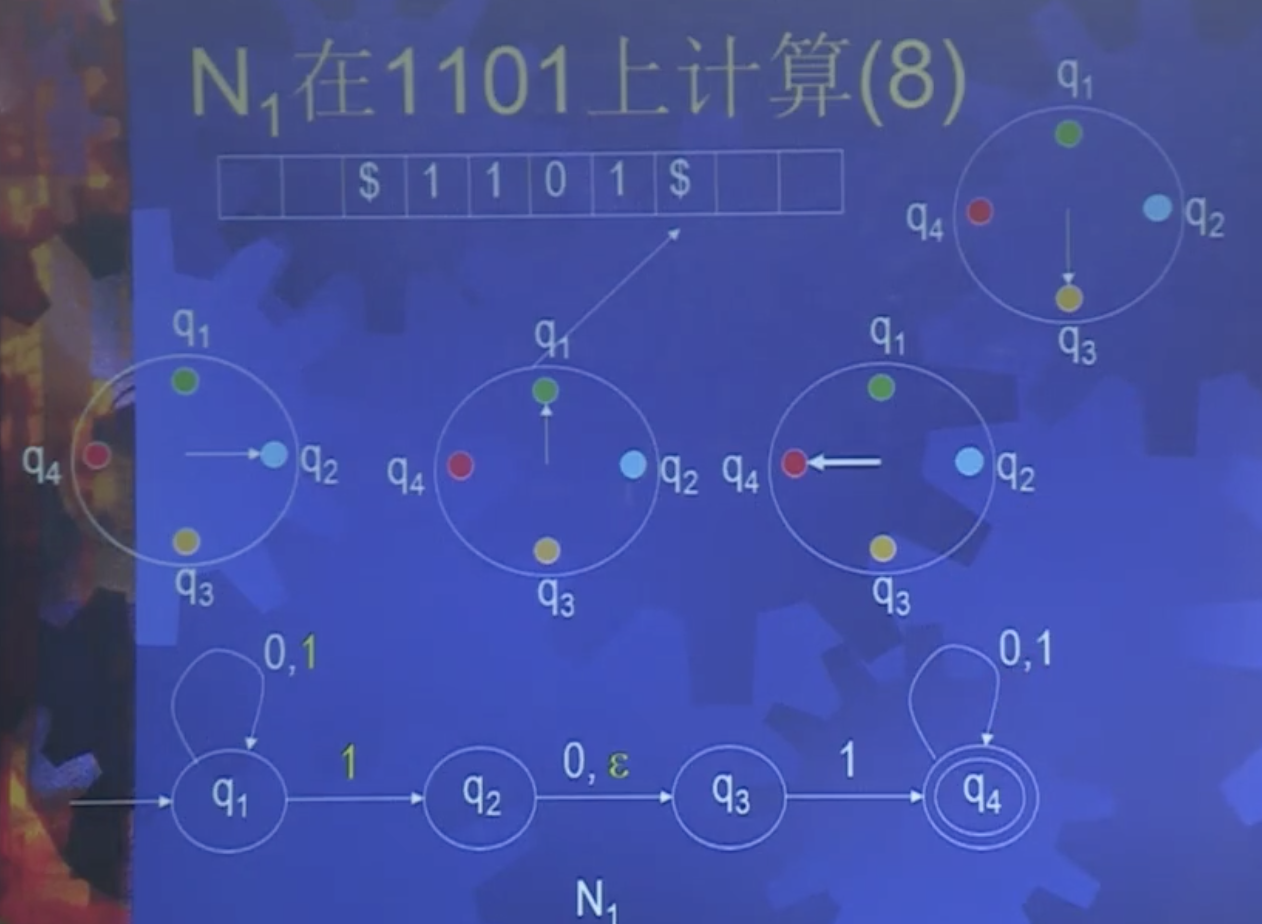
非确定性有穷自动机

特点：下一个状态可以不唯一确定：

$\epsilon$ 移动或每一步有多个选择，产生不同的备份
无法移动备份消失
一个备份接受则接受
自动机描述简单，减少状态数，分析麻烦

NFA 与 DFA 的等价性

$\epsilon$ 闭包：每个状态子集合，经 $\epsilon$ 移动可以达到的新状态子集合。

定理2.19：每台 NFA 都有等价 DFA
思路：给定NFA，构造 DFA 记住 NFA 的所有分支，设有 k 个状态则有 $2^k$ 个不同状态子集合。
证明：设 NFA $N=(Q,\Sigma,\delta,q_0,F)$ ，
构造 DFA $M(Q',\Sigma,\delta',q_0',F')$ ， $L(M)=L(N)$

$Q'=P(Q)$ ，原来状态的幂集
$\delta'(R, a)=\bigcup_{r\in R}E(\delta(r,a))$ , E 为 $\epsilon$ 闭包，从一个 $\epsilon$ 闭包转移到另一个 $\epsilon$ 闭包
$q_0'=E(\{q_0\})$
$F'=\{R\in Q'|R\cap F\neq \emptyset\}$

推论2.20：一个语言是正则的，当且仅当有一台 NFA 识别它。

正则表达式

引理2.29：正则表达式描述正则语言
证明：先验证小的正则表达式可以用 NFA 表示，再使用正则运算进行归纳。

引理2.32：正则语言可以用正则表达式描述
思路：

GNFA：箭头标号是正则表达式
从 DFA 构造等价的 GNFA
从 GNFA 构造等价的正则表达式

证明：

设正则语言 A 被 DFA M 识别
把 M 转换成等价的 GNFA G
把 G 转换成等价的正则表达式

非正则语言

定理2.37(泵引理)：设 A 是正则语言，则存在常数 p (泵长度)，使得若 $s\in A$ ，且 $|s|\geq p$ ，则 $s=xyz$ ，且满足下述条件：

任给的 $i\geq 0, xy^iz\in A$
$|y|>0$
$|xy|\leq p$

证明： $p$ 为确定性有穷自动机的状态数，长度大于等于 $p$ 的串至少经过 $p+1$ 个状态。

使用方式：

假设 $B$ 是正则的，设 $p$ 是泵长度
取 $s\in B, |s|\geq p$
根据泵引理， $s=xyz$ $s = x y z$
1. 任给的 $i\geq 0, xy^iz\in A$
2. $|y|>0$
3. $|xy|\leq p$
证明存在 $i\geq 0$ ，使得 $xy^iz\in B$ ，矛盾。