[计算理论基础] 可计算问题

正则语言的可判定问题

$A_{DFA}, A_{NFA}, A_{REX}, E_{DFA}, EQ_{DFA}$

DFA 接受性问题 - 可判定

检查输入是否是 DFA 和串
直接模拟 DFA，其一定可以停机

NFA 接受性问题 - 可判定

检查输入
选择一种方法
将 NFA 转为 DFA (多项式时间)
使用 NTM 模拟 NFA

正则表达式的派生问题 - 可判定

检查输入
将正则表达式转为 DFA 使用前面的机器判定

DFA 的空性问题 - 可判定

标记算法，DFA 有有限个状态。首先标记初始状态，每个状态如果前面的状态被标记则也标记该状态，直到没有新的状态被标记，如果接受状态标记则拒绝。

DFA 的等价问题

对于两个语言A、B计算其对称差(封闭操作)得到 DFA C，根据 C 是否为空接受或拒绝 A、B 等价。

上下文无关语言的可判定问题

$A_{CFG}, E_{CFG}, EQ_{CFG}$ , $ALL_{CFG}$ , 每个 CFL 是可判定的

CFG 的接受性问题 - 可判定

采用 CNF，派生长度为 n 的串需要 $2n-1$ 步，检查所有长度为 $2n-1$ 的派生。如果有一个产生 w 接受否则拒绝。

CFG 的空性问题 - 可判定

标记算法。从终结符开始标记，对于存在的规则 $A\to U_1U_2...U_k$ 如果右侧都已经标记则对变元 $A$ 进行标记。如果起始变元没有被标记则接受，否则拒绝。

CFG 的满性问题 - 不可判定

思路：从 $A_{TM}$ 出发的计算历史的规约。设计文法 G 产生所有不是 M 在 w 上接受历史的串，这样，当 M 接受 w 时，L(G) 就不满 ( 因为存在 M 在 w 上的接受历史 )，此时 $ALL_{CFG}$ 就会拒绝，反之如果 M 不接受 w，则没有 M 在 w 上的接受历史，此时 L(G) 为满， $ALL_{CFG}$ 就会接受，依次判定 $A_{TM}$
证明：按照思路构建判定 $ALL_{CFG}$ 的 F，和一个根据 M 和 w 构建的机器 T，T 接受所有不是 M 在 w 上接受历史的串。将 $<T>$ 输入 F，如果 F 接受，说明 L(T) 为满，说明没有 M 在 w 上的接受历史，所以拒绝，反之接受。

CFG 的等价性问题 - 不可判定

将 CFG 满性问题规约到 CFG 等价性问题，构造识别所有串的文法 FU，对于输入的文法 G，将 $<FU, G>$ 输入 $EQ_{CFG}$ ，如果接受则接受，如果拒绝则拒绝。

每个 CFL 是可判定的 - 可判定的

对于 CFL A，得到 CFG G 是它的文法，对于输入串 w 在 $A_{CFG}$ 运行 $<G,w>$ ，如果接受则接受，否则拒绝。

不可计算问题

推论5.15：存在非图灵可识别语言
证明：全体图灵可识别语言构成可数集，前提语言是非可数集

定理5.9： $A_{TM}$ 是不可判定的
思路： $D_{TM}=\{<M>|TM\ M\ accept\ <M>\}$ ，使用对角线方法证明 $D_{TM}$ 不可判定。 对角化方法。
证明：假设存在 H 判定 $A_{TM}$ 。
构造 D 输入 $<M>$ ，如果 H 接受 $<M, <M>>$ 则 D 拒绝，否则接受，总的来说D 输出和 H 相反的结果。
现将 $<D>$ 输入 D 中，如果 D 接受 $<D>$ ，则 H 拒绝 $<D, <D>>$ ,即 D 不接受 $<D>$ ，矛盾。
关键在于 D 本身是图灵机，他将出现在 H 的结果列表中，但 H 对角线的结果和 D 得到的结果是互补的于是得到矛盾。

定理5.16： $A$ 可判定 $\Leftrightarrow$ $A$ 和 $\overline A$ 都是可识别的。
思路：

$\Rightarrow$ - 如果 $A$ 可判定，则 $\overline A$ 也可判定 (布尔运算封闭)，所以 $\overline A$ 可识别
$\Leftarrow$ - 如果 $A$ 和 $\overline A$ 都可识别，则根据当 $A$ 接受时接受， $overline A$ 接受时拒绝(此时说明 $A$ 不接受)。

推论5.17： $\overline A_{TM}$ 是图灵不可识别的

图灵机的不可计算问题

定理6.1： $HALT_{TM}$ 是不可判定的
思路：假设这个问题可判定，证明 $A_{TM}$ 可判定，矛盾。
证明：对于输入 $<M, w>$ ，使用 $HALT_{TM}$ 判定是否不停机，如果不停机就拒绝，否则模拟 M 输入 w，如果接受就接受，如果拒绝就拒绝。

定理： $E_{TM}$ 是不可判定的
思路：使用该语言使 $A_{TM}$ 可判定，矛盾。
证明：构造 $M_1$ =“

如果 $x\neq w$ ，则拒绝
如果 $x=w$ ，则在 x 上运行 M，当M接受时就接受”

对于输入 $<M,w>$ ，首先构造 $M_1$ ，如果 E 拒绝 $M_1$ ，说明其不为空，即 M 接受 w，反之，如果 E 接受 $M_1$ 则其为空，说明 M 不接受 w， $M_1$ 只在 M 接受 w 时有值，否则为空。

定理6.3： $REGULAR_{TM}$ 是不可判定的
思路：使用该语言使 $A_{TM}$ 可判定，矛盾。
证明：构造 $M_2$ =“

如果x具有 $0^n1^n$ 形式，接受
如果不是这种形式，就用 w 在 M 上运行，如果 M 接受 w，则接受”

对于输入 $<M,w>$ ，首先构造 $M_2$ ，用 R 接受输入 $<M_2>$ ，如果 R 接受，则说明 $M_2$ 的语言是正则的，即 M 接受 w，此时其代表的语言是 $\Sigma^*$ ，反之，其只接受 $0^n1^n$ 该语言是非正则的，所以 M 没有接受 w，据此进行接受或拒绝。

定理6.4： $EQ_{TM}$ 是不可判定的
思路：使用该语言使 $E_{TM}$ 可判定，矛盾。
证明：将一个空图灵机作为 EQ 的一个输入，即可判断图灵空性问题。

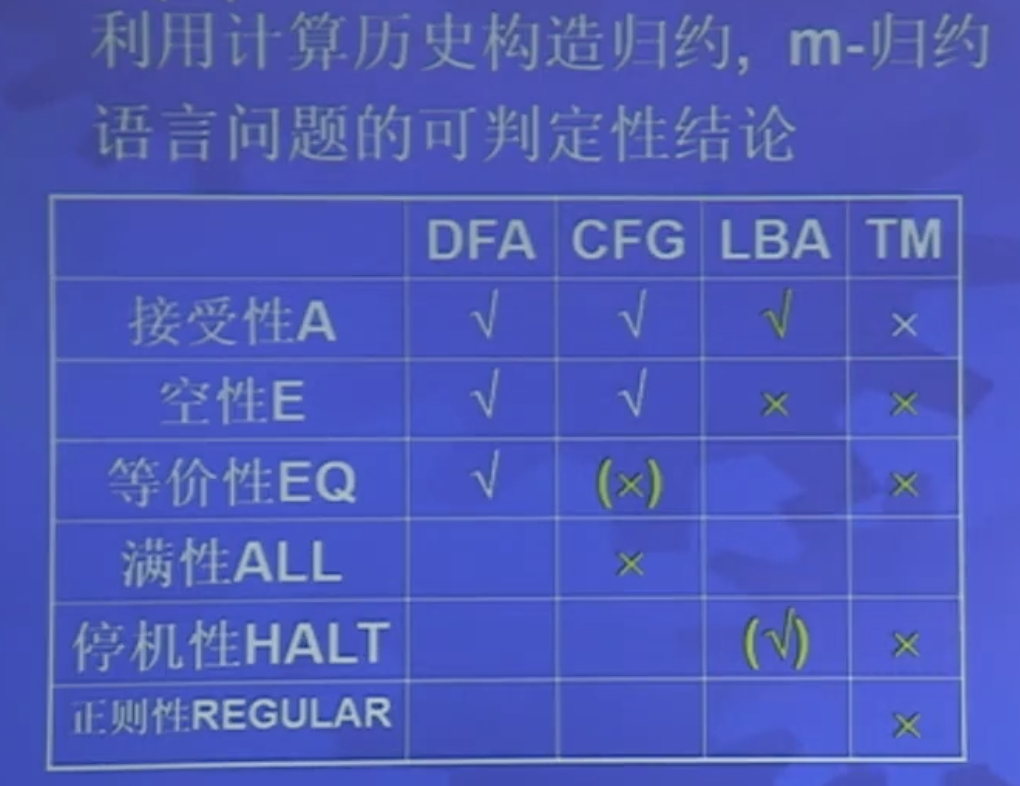
可判定性总结

	DFA	CFG	TM
接受性	√	√	×
空性	√	√	×
等价性	√	×	×

基于计算历史的规约

接受计算历史：格局序列 $C_1,C_2,...,C_k$ ，其中 $C_1$ 是初始格局，每个 $C_i\to C_{i+1}$ 都是合法转移， $C_k$ 是接受格局。计算历史都是有穷序列。

线性界限自动机 (LBA)

带头不能移出输入区常数倍的图灵机。识别上下文有关语言。

定理6.8： $A_{LBA}$ 是可判定的
思路：对于有 q 个状态和 g 个带符号的 LBA，对于长度为 n 的带子，M 恰有 $qng^n$ 个格局。由于格局数有限，所以当格局数超过这个值时拒绝 ( 解决停机问题 )。非确定 LBA 格局数为 $qng^n!$

定理6.9： $E_{LBA}$ 是不可判定的
思路：使用从 $A_{TM}$ 出发的规约。使用 M，w，构造 LBA B，使得 M 接受 w 时 L(B) 非空，这时候可以使 L(B) 为接受计算历史，这样，当 M 接受 w 时，说明 L(B) 不为空，此时使用 $E_{LBA}$ 判定 B 即可知道 M 是否接受 w。
证明：构造识别计算历史的 TM B。基于思路设计图灵机。

规约的定义、性质

可计算函数：对于某个函数 f，如果存在图灵机 M，使得在每个输入上停机且 f(w) 出现在带上，则 f 是可计算函数。

m规约：存在 f 使得对于 x：

$x\in A \Leftrightarrow f(x) \in B$

即 A 可 m 规约到 B，记作

$A\leq_m B$

称函数 f 为从 A 到 B 的规约，记作

$B\leq_m B\ via\ f$

定理6.16：若 $A\leq_m B$ ，且 B 可判定，则 A 可判定。
思路：使用规约 f 将 A 转为 B，并根据 B 的输出输出。

定理6.1： $A_{TM}\leq_m HALT_{TM}\ via\ f$
思路：将判断 M 接受还是拒绝 w 的问题变为机器接受 w 后能不能停机问题。
证明：构造 F 计算 f = “

构造下面机器 T=“

在 x 上运行 M
若 M 接受，则接受
若 M 拒绝，则进入死循环
”

输出 $<T, w>$ ”

RICE 定理

若 S 是非平凡指标集，则 S 不可判定。
S 非平凡指 $S\neq \emptyset, S\neq \Sigma^*$
S 是指标集指 S 是 TM 编码的集合，且

$<M_1>\in S\wedge L(M_1)=L(M_2) \Rightarrow <M_2> \in S$